Wave Function Collapse
About this tutorial
This tutorial is free and open source, and all code uses the MIT license - so you are free to do with it as you like. My hope is that you will enjoy the tutorial, and make great games!
If you enjoy this and would like me to keep writing, please consider supporting my Patreon.
A few years ago, Wave Function Collapse (WFC) exploded onto the procedural generation scene. Apparently magical, it took images in - and made a similar image. Demos showed it spitting out great looking game levels, and the amazing Caves of Qud started using it for generating fun levels. The canonical demonstrations - along with the original algorithm in C# and various explanatory links/ports - may be found here.
In this chapter, we're going to implement Wave Function Collapse from scratch - and apply it to making fun Roguelike levels. Note that there is a crate with the original algorithm available (wfc, accompanied by wfc-image); it seemed pretty good in testing, but I had problems making it work with Web Assembly. I also didn't feel that I was really teaching the algorithm by saying "just import this". It's a longer chapter, but by the end you should feel comfortable with the algorithm.
So what does WFC really do?
Wave Function Collapse is unlike the map generation algorithms we've used so far in that it doesn't actually make maps. It takes source data in (we'll use other maps!), scans them, and builds a new map featuring elements made exclusively from the source data. It operates in a few phases:
- It reads the incoming data. In the original implementation, this was a PNG file. In our implementation, this is a
Mapstructure like others we've worked with; we'll also implement a REX Paint reader to load maps. - It divides the source image into "tiles", and optionally makes more tiles by mirroring the tiles it reads along one or two axes.
- It either loads or builds a "constraints" graph. This is a set of rules specifying which tiles can go next to each other. In an image, this may be derived from tile adjacency. In a Roguelike map, connectivity of exits is a good metric. For a tile-based game, you might carefully build a layout of what can go where.
- It then divides the output image into tile-sized chunks, and sets them all to "empty". The first tile placed will be pretty random, and then it selects areas and examines tile data that is already known - placing down tiles that are compatible with what is already there. Eventually, it's placed all of the tiles - and you have a map/image!
The name "Wave Function Collapse" refers to the Quantum Physics idea that a particle may have not actually have a state until you look at it. In the algorithm, tiles don't really coalesce into being until you pick one to examine. So there is a slight similarity to Quantum Physics. In reality, though - the name is a triumph of marketing. The algorithm is what is known as a solver - given a set of constraints, it iterates through possible solutions until the constraints are solved. This isn't a new concept - Prolog is an entire programming language based around this idea, and it first hit the scene in 1972. So in a way, it's older than me!
Getting started: Rust support for complex modules
All our previous algorithms were small enough to fit into one source code file, without too much paging around to find the relevant bit of code. Wave Function Collapse is complicated enough that it deserves to be broken into multiple files - in much the same was as the map_builders module was broken into a module - WFC will be divided into its own module. The module will still live inside map_builders - so in a way it's really a sub-module.
Rust makes it pretty easy to break any module into multiple files: you create a directory inside the parent module, and put a file in it called mod.rs. You can then put more files in the folder, and so long as you enable them (with mod myfile) and use the contents (with use myfile::MyElement) it works just like a single file.
So to get started, inside your map_builders directory - make a new directory called waveform_collapse. Add a file, mod.rs into it. You should have a source tree like this:
\ src
\ map_builders
\ waveform_collapse
+ mod.rs
bsp_dungeon.rs
(etc)
main.rs
(etc)
We'll populate mod.rs with a skeletal implementation similar to previous chapters:
#![allow(unused)] fn main() { use super::{MapBuilder, Map, TileType, Position, spawner, SHOW_MAPGEN_VISUALIZER, generate_voronoi_spawn_regions, remove_unreachable_areas_returning_most_distant}; use rltk::RandomNumberGenerator; use specs::prelude::*; pub struct WaveformCollapseBuilder { map : Map, starting_position : Position, depth: i32, history: Vec<Map>, noise_areas : HashMap<i32, Vec<usize>> } impl MapBuilder for WaveformCollapseBuilder { fn get_map(&self) -> Map { self.map.clone() } fn get_starting_position(&self) -> Position { self.starting_position.clone() } fn get_snapshot_history(&self) -> Vec<Map> { self.history.clone() } fn build_map(&mut self) { self.build(); } fn spawn_entities(&mut self, ecs : &mut World) { for area in self.noise_areas.iter() { spawner::spawn_region(ecs, area.1, self.depth); } } fn take_snapshot(&mut self) { if SHOW_MAPGEN_VISUALIZER { let mut snapshot = self.map.clone(); for v in snapshot.revealed_tiles.iter_mut() { *v = true; } self.history.push(snapshot); } } } impl WaveformCollapseBuilder { pub fn new(new_depth : i32) -> WaveformCollapseBuilder { WaveformCollapseBuilder{ map : Map::new(new_depth), starting_position : Position{ x: 0, y : 0 }, depth : new_depth, history: Vec::new(), noise_areas : HashMap::new() } } fn build(&mut self) { let mut rng = RandomNumberGenerator::new(); // TODO: Builder goes here // Find a starting point; start at the middle and walk left until we find an open tile self.starting_position = Position{ x: self.map.width / 2, y : self.map.height / 2 }; /*let mut start_idx = self.map.xy_idx(self.starting_position.x, self.starting_position.y); while self.map.tiles[start_idx] != TileType::Floor { self.starting_position.x -= 1; start_idx = self.map.xy_idx(self.starting_position.x, self.starting_position.y); }*/ self.take_snapshot(); // Find all tiles we can reach from the starting point let exit_tile = remove_unreachable_areas_returning_most_distant(&mut self.map, start_idx); self.take_snapshot(); // Place the stairs self.map.tiles[exit_tile] = TileType::DownStairs; self.take_snapshot(); // Now we build a noise map for use in spawning entities later self.noise_areas = generate_voronoi_spawn_regions(&self.map, &mut rng); } } }
We'll also modify map_builders/mod.rs's random_builder function to always return the algorithm we're currently working with:
#![allow(unused)] fn main() { pub fn random_builder(new_depth: i32) -> Box<dyn MapBuilder> { /* let mut rng = rltk::RandomNumberGenerator::new(); let builder = rng.roll_dice(1, 16); match builder { 1 => Box::new(BspDungeonBuilder::new(new_depth)), 2 => Box::new(BspInteriorBuilder::new(new_depth)), 3 => Box::new(CellularAutomataBuilder::new(new_depth)), 4 => Box::new(DrunkardsWalkBuilder::open_area(new_depth)), 5 => Box::new(DrunkardsWalkBuilder::open_halls(new_depth)), 6 => Box::new(DrunkardsWalkBuilder::winding_passages(new_depth)), 7 => Box::new(DrunkardsWalkBuilder::fat_passages(new_depth)), 8 => Box::new(DrunkardsWalkBuilder::fearful_symmetry(new_depth)), 9 => Box::new(MazeBuilder::new(new_depth)), 10 => Box::new(DLABuilder::walk_inwards(new_depth)), 11 => Box::new(DLABuilder::walk_outwards(new_depth)), 12 => Box::new(DLABuilder::central_attractor(new_depth)), 13 => Box::new(DLABuilder::insectoid(new_depth)), 14 => Box::new(VoronoiCellBuilder::pythagoras(new_depth)), 15 => Box::new(VoronoiCellBuilder::manhattan(new_depth)), _ => Box::new(SimpleMapBuilder::new(new_depth)) }*/ Box::new(WaveformCollapseBuilder::new(new_depth)) } }
This will give you an empty map (all walls) if you cargo run it - but it's a good starting point.
Loading the source image - REX Paint
You may remember back in section 2 we loaded a REX Paint file to use as the main menu screen. We're going to do similar here, but we're going to turn it into a playable map. It's a deliberately odd map to help illustrate what you can do with this algorithm. Here's the original in REX Paint:
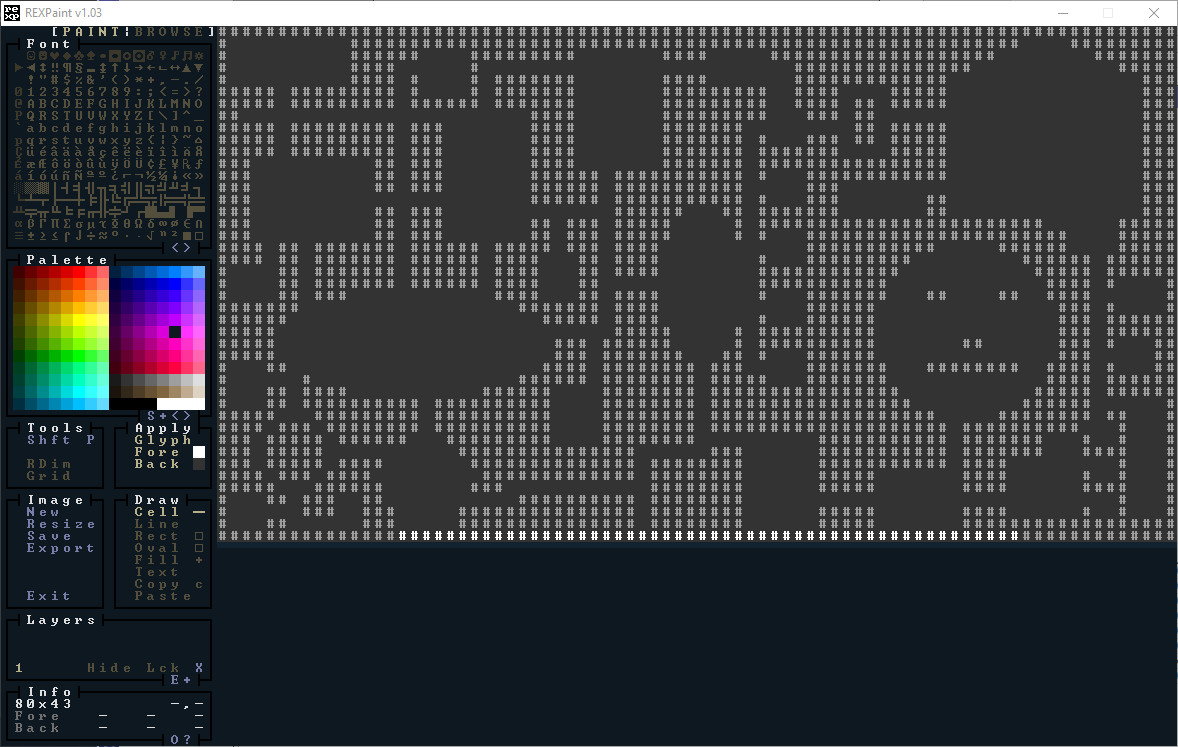 .
.
I've tried to include some interesting shapes, a silly face, and plenty of corridors and different sized rooms. Here's a second REX Paint file, designed to be more like the old board game The Sorcerer's Cave, of which the algorithm reminds me - tiles with 1 exit, 2 exits, 3 exits and 4. It would be easy to make these prettier, but we'll keep it simple for demonstration purposes.
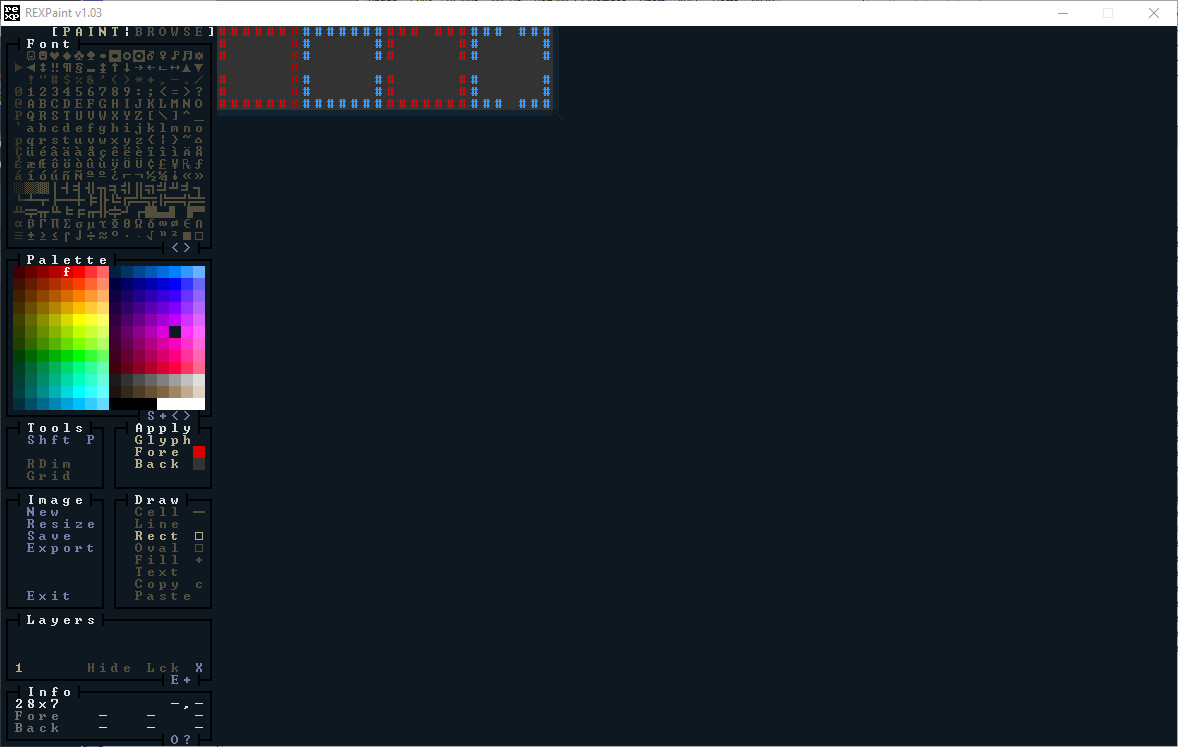 .
.
These files are found in the resources directory, as wfc-demo1.xp and wfc-demo2.xp. One thing I love about REX Paint: the files are tiny (102k and 112k respectively). To make accessing them easier - and avoid having to ship them with the executable when you publish your finished game, we'll embed them into our game. We did this previously for the main menu. Modify rex_assets.xp to include the new files:
#![allow(unused)] fn main() { use rltk::{rex::XpFile}; rltk::embedded_resource!(SMALL_DUNGEON, "../../resources/SmallDungeon_80x50.xp"); rltk::embedded_resource!(WFC_DEMO_IMAGE1, "../../resources/wfc-demo1.xp"); rltk::embedded_resource!(WFC_DEMO_IMAGE2, "../../resources/wfc-demo2.xp"); pub struct RexAssets { pub menu : XpFile } impl RexAssets { #[allow(clippy::new_without_default)] pub fn new() -> RexAssets { rltk::link_resource!(SMALL_DUNGEON, "../../resources/SmallDungeon_80x50.xp"); rltk::link_resource!(WFC_DEMO_IMAGE1, "../../resources/wfc-demo1.xp"); rltk::link_resource!(WFC_DEMO_IMAGE2, "../../resources/wfc-demo2.xp"); RexAssets{ menu : XpFile::from_resource("../../resources/SmallDungeon_80x50.xp").unwrap() } } } }
Finally, we should load the map itself! Inside the waveform_collapse directory, make a new file: image_loader.rs:
#![allow(unused)] fn main() { use rltk::rex::XpFile; use super::{Map, TileType}; /// Loads a RexPaint file, and converts it into our map format pub fn load_rex_map(new_depth: i32, xp_file : &XpFile) -> Map { let mut map : Map = Map::new(new_depth); for layer in &xp_file.layers { for y in 0..layer.height { for x in 0..layer.width { let cell = layer.get(x, y).unwrap(); if x < map.width as usize && y < map.height as usize { let idx = map.xy_idx(x as i32, y as i32); match cell.ch { 32 => map.tiles[idx] = TileType::Floor, // # 35 => map.tiles[idx] = TileType::Wall, // # _ => {} } } } } } map } }
This is really simple, and if you remember the main menu graphic tutorial it should be quite self-explanatory. This function:
- Accepts arguments for
new_depth(because maps want it) and a reference to anXpFile- a REX Paint map. It will be made completely solid, walls everywhere by the constructor. - It creates a new map, using the
new_depthparameter. - For each layer in the REX Paint file (there should be only one at this point):
- For each
yandxon that layer:- Load the tile information for that coordinate.
- Ensure that we're within the map boundaries (in case we have a mismatch in sizes).
- Calculate the
tilesindex for the cell. - Match on the cell glyph; if its a
#(35) we place a wall, if its a space (32) we place a floor.
- For each
Now we can modify our build function (in mod.rs) to load the map:
#![allow(unused)] fn main() { fn build(&mut self) { let mut rng = RandomNumberGenerator::new(); self.map = load_rex_map(self.depth, &rltk::rex::XpFile::from_resource("../../resources/wfc-demo1.xp").unwrap()); self.take_snapshot(); // Find a starting point; start at the middle and walk left until we find an open tile self.starting_position = Position{ x: self.map.width / 2, y : self.map.height / 2 }; ... }
At the top, we have to tell it to use the new image_loader file:
#![allow(unused)] fn main() { mod image_loader; use image_loader::*; }
Note that we're not putting pub in front of these: we're using them, but not exposing them outside of the module. This helps us keep our code clean, and our compile times short!
In and of itself, this is cool - we can now load any REX Paint designed level and play it! If you cargo run now, you'll find that you can play the new map:
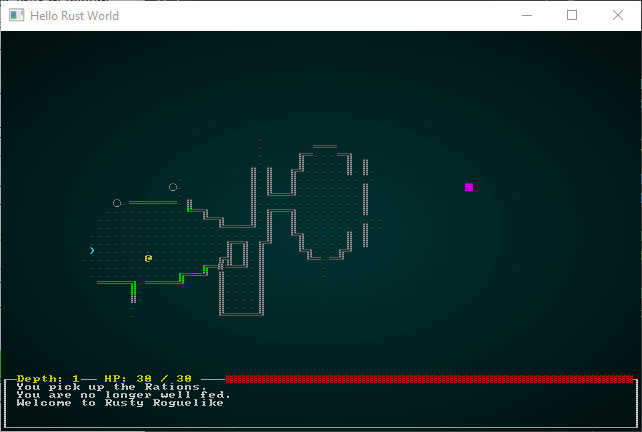 .
.
We'll make use of this in later chapters for vaults, prefabs and pre-designed levels - but for now, we'll just use it as source data for later in the Wave Function Collapse implementation.
Carving up our map into tiles
We discussed earlier that WFC works by carving the original image into chunks/tiles, and optionally flipping them in different directions. It does this as the first part of building constraints - how the map can be laid out. So now we need to start carving up our image.
We'll start by picking a tile size (we're going to call it chunk_size). We'll make it a constant for now (it'll become tweakable later), and start with a size of 7 - because that was the size of the tiles in our second REX demo file. We'll also call a function we'll write in a moment:
#![allow(unused)] fn main() { fn build(&mut self) { let mut rng = RandomNumberGenerator::new(); const CHUNK_SIZE :i32 = 7; self.map = load_rex_map(self.depth, &rltk::rex::XpFile::from_resource("../../resources/wfc-demo2.xp").unwrap()); self.take_snapshot(); let patterns = build_patterns(&self.map, CHUNK_SIZE, true, true); ... }
Since we're dealing with constraints, we'll make a new file in our map_builders/waveform_collapse directory - constraints.rs. We're going to make a function called build_patterns:
#![allow(unused)] fn main() { use super::{TileType, Map}; use std::collections::HashSet; pub fn build_patterns(map : &Map, chunk_size: i32, include_flipping: bool, dedupe: bool) -> Vec<Vec<TileType>> { let chunks_x = map.width / chunk_size; let chunks_y = map.height / chunk_size; let mut patterns = Vec::new(); for cy in 0..chunks_y { for cx in 0..chunks_x { // Normal orientation let mut pattern : Vec<TileType> = Vec::new(); let start_x = cx * chunk_size; let end_x = (cx+1) * chunk_size; let start_y = cy * chunk_size; let end_y = (cy+1) * chunk_size; for y in start_y .. end_y { for x in start_x .. end_x { let idx = map.xy_idx(x, y); pattern.push(map.tiles[idx]); } } patterns.push(pattern); if include_flipping { // Flip horizontal pattern = Vec::new(); for y in start_y .. end_y { for x in start_x .. end_x { let idx = map.xy_idx(end_x - (x+1), y); pattern.push(map.tiles[idx]); } } patterns.push(pattern); // Flip vertical pattern = Vec::new(); for y in start_y .. end_y { for x in start_x .. end_x { let idx = map.xy_idx(x, end_y - (y+1)); pattern.push(map.tiles[idx]); } } patterns.push(pattern); // Flip both pattern = Vec::new(); for y in start_y .. end_y { for x in start_x .. end_x { let idx = map.xy_idx(end_x - (x+1), end_y - (y+1)); pattern.push(map.tiles[idx]); } } patterns.push(pattern); } } } // Dedupe if dedupe { rltk::console::log(format!("Pre de-duplication, there are {} patterns", patterns.len())); let set: HashSet<Vec<TileType>> = patterns.drain(..).collect(); // dedup patterns.extend(set.into_iter()); rltk::console::log(format!("There are {} patterns", patterns.len())); } patterns } }
That's quite the mouthful of a function, so let's walk through it:
- At the top, we're importing some items from elsewhere in the project:
Map,TileType, and the built-in collectionHashMap. - We declare our
build_patternsfunction, with parameters for a reference to the source map, thechunk_sizeto use (tile size), and flags (boolvariables) forinclude_flippinganddedupe. These indicate which features we'd like to use when reading the source map. We're returning avector, containing a series ofvectors of differentTileTypes. The outer container holds each pattern. The inner vector holds theTileTypes that make up the pattern itself. - We determine how many chunks there are in each direction and store it in
chunks_xandchunks_y. - We create a new
vectorcalledpatterns. This will hold the result of the function; we don't declare it's type, because Rust is smart enough to see that we're returning it at the end of the function - and can figure out what type it is for us. - We iterate every vertical chunk in the variable
cy:- We iterate every horizontal chunk in the variable
cx:- We make a new
vectorto hold this pattern. - We calculate
start_x,end_x,start_yandend_yto hold the four corner coordinates of this chunk - on the original map. - We iterate the pattern in
y/xorder (to match our map format), read in theTileTypeof each map tile within the chunk, and add it to the pattern. - We push the pattern to the
patternsresult vector. - If
include_flippingis set totrue(because we'd like to flip our tiles, making more tiles!):- Repeat iterating
y/xin different orders, giving 3 more tiles. Each is added to thepatternsresult vector.
- Repeat iterating
- We make a new
- We iterate every horizontal chunk in the variable
- If
dedupeis set, then we are "de-duplicating" the pattern buffer. Basically, removing any pattern that occurs more than once. This is good for a map with lots of wasted space, if you don't want to make an equally sparse result map. We de-duplicate by adding the patterns into aHashMap(which can only store one of each entry) and then reading it back out again.
For this to compile, we have to make TileType know how to convert itself into a hash. HashMap uses "hashes" (basically a checksum of the contained values) to determine if an entry is unique, and to help find it. In map.rs, we can simply add one more derived attribute to the TileType enumeration:
#![allow(unused)] fn main() { #[derive(PartialEq, Eq, Hash, Copy, Clone, Serialize, Deserialize)] pub enum TileType { Wall, Floor, DownStairs } }
This code should get you every 7x7 tile within your source file - but it'd be great to be able to prove that it works! As Reagan's speech-writer once wrote, Trust - But Verify. In constraints.rs, we'll add another function: render_pattern_to_map:
#![allow(unused)] fn main() { fn render_pattern_to_map(map : &mut Map, pattern: &Vec<TileType>, chunk_size: i32, start_x : i32, start_y: i32) { let mut i = 0usize; for tile_y in 0..chunk_size { for tile_x in 0..chunk_size { let map_idx = map.xy_idx(start_x + tile_x, start_y + tile_y); map.tiles[map_idx] = pattern[i]; map.visible_tiles[map_idx] = true; i += 1; } } } }
This is pretty simple: iterate the pattern, and copy to a location on the map - offset by the start_x and start_y coordinates. Note that we're also marking the tile as visible - this will make the renderer display our tiles in color.
Now we just need to display our tiles as part of the snapshot system. In waveform_collapse/mod.rs add a new function as part of the implementation of WaveformCollapseBuilder (underneath build). It's a member function because it needs access to the take_snapshot command:
#![allow(unused)] fn main() { fn render_tile_gallery(&mut self, patterns: &Vec<Vec<TileType>>, chunk_size: i32) { self.map = Map::new(0); let mut counter = 0; let mut x = 1; let mut y = 1; while counter < patterns.len() { render_pattern_to_map(&mut self.map, &patterns[counter], chunk_size, x, y); x += chunk_size + 1; if x + chunk_size > self.map.width { // Move to the next row x = 1; y += chunk_size + 1; if y + chunk_size > self.map.height { // Move to the next page self.take_snapshot(); self.map = Map::new(0); x = 1; y = 1; } } counter += 1; } self.take_snapshot(); } }
Now, we need to call it. In build:
#![allow(unused)] fn main() { let patterns = build_patterns(&self.map, CHUNK_SIZE, true, true); self.render_tile_gallery(&patterns, CHUNK_SIZE); }
Also, comment out some code so that it doesn't crash from not being able to find a starting point:
#![allow(unused)] fn main() { let mut start_idx = self.map.xy_idx(self.starting_position.x, self.starting_position.y); /*while self.map.tiles[start_idx] != TileType::Floor { self.starting_position.x -= 1; start_idx = self.map.xy_idx(self.starting_position.x, self.starting_position.y); }*/ }
If you cargo run now, it'll show you the tile patterns from map sample 2:
 .
.
Notice how flipping has given us multiple variants of each tile. If we change the image loading code to load wfc-demo1 (by changing the loader to self.map = load_rex_map(self.depth, &rltk::rex::XpFile::from_resource("../../resources/wfc-demo1.xp").unwrap());), we get chunks of our hand-drawn map:
 .
.
Building the constraints matrix
Now we need to begin to tell the algorithm how it can place tiles next to one another. We could go for a simple "what's next to it on the original image?" algorithm, but that would ignore a key factor in roguelike maps: connectivity. We're far more interested in the ability to go from point A to point B than we are in overall aesthetics! So we need to write a constraint builder that takes into account connectivity.
We'll start by extending builder in mod.rs to call a hypothetical function we'll implement in a second:
#![allow(unused)] fn main() { let patterns = build_patterns(&self.map, CHUNK_SIZE, true, true); self.render_tile_gallery(&patterns, CHUNK_SIZE); let constraints = patterns_to_constraints(patterns, CHUNK_SIZE); }
This gives us the signature of a new method, patterns_to_constraints to add to constraints.rs. We're also going to need a new type and a helper function. We'll use these in other places, so we're going to add a new file to the waveform_collapse folder - common.rs.
#![allow(unused)] fn main() { use super::TileType; #[derive(PartialEq, Eq, Hash, Clone)] pub struct MapChunk { pub pattern : Vec<TileType>, pub exits: [Vec<bool>; 4], pub has_exits: bool, pub compatible_with: [Vec<usize>; 4] } pub fn tile_idx_in_chunk(chunk_size: i32, x:i32, y:i32) -> usize { ((y * chunk_size) + x) as usize } }
We're defining MapChunk to be a structure, containing the actual pattern, a structure of exits (more on that in a moment), a bool to say we have any exits, and a structure called compatible_with (more on that in a second, too). We're also defining tile_idx_in_chunk - which is just like map.xy_idx - but constrained to a small tile type.
Now we'll write patterns_to_constraints in constraints.rs:
#![allow(unused)] fn main() { pub fn patterns_to_constraints(patterns: Vec<Vec<TileType>>, chunk_size : i32) -> Vec<MapChunk> { // Move into the new constraints object let mut constraints : Vec<MapChunk> = Vec::new(); for p in patterns { let mut new_chunk = MapChunk{ pattern: p, exits: [ Vec::new(), Vec::new(), Vec::new(), Vec::new() ], has_exits : true, compatible_with: [ Vec::new(), Vec::new(), Vec::new(), Vec::new() ] }; for exit in new_chunk.exits.iter_mut() { for _i in 0..chunk_size { exit.push(false); } } let mut n_exits = 0; for x in 0..chunk_size { // Check for north-bound exits let north_idx = tile_idx_in_chunk(chunk_size, x, 0); if new_chunk.pattern[north_idx] == TileType::Floor { new_chunk.exits[0][x as usize] = true; n_exits += 1; } // Check for south-bound exits let south_idx = tile_idx_in_chunk(chunk_size, x, chunk_size-1); if new_chunk.pattern[south_idx] == TileType::Floor { new_chunk.exits[1][x as usize] = true; n_exits += 1; } // Check for west-bound exits let west_idx = tile_idx_in_chunk(chunk_size, 0, x); if new_chunk.pattern[west_idx] == TileType::Floor { new_chunk.exits[2][x as usize] = true; n_exits += 1; } // Check for east-bound exits let east_idx = tile_idx_in_chunk(chunk_size, chunk_size-1, x); if new_chunk.pattern[east_idx] == TileType::Floor { new_chunk.exits[3][x as usize] = true; n_exits += 1; } } if n_exits == 0 { new_chunk.has_exits = false; } constraints.push(new_chunk); } // Build compatibility matrix let ch = constraints.clone(); for c in constraints.iter_mut() { for (j,potential) in ch.iter().enumerate() { // If there are no exits at all, it's compatible if !c.has_exits || !potential.has_exits { for compat in c.compatible_with.iter_mut() { compat.push(j); } } else { // Evaluate compatibilty by direction for (direction, exit_list) in c.exits.iter_mut().enumerate() { let opposite = match direction { 0 => 1, // Our North, Their South 1 => 0, // Our South, Their North 2 => 3, // Our West, Their East _ => 2 // Our East, Their West }; let mut it_fits = false; let mut has_any = false; for (slot, can_enter) in exit_list.iter().enumerate() { if *can_enter { has_any = true; if potential.exits[opposite][slot] { it_fits = true; } } } if it_fits { c.compatible_with[direction].push(j); } if !has_any { // There's no exits on this side, we don't care what goes there for compat in c.compatible_with.iter_mut() { compat.push(j); } } } } } } constraints } }
This is a really big function, but clearly broken down into sections. Let's take the time to walk through what it actually does:
- It accepts a first parameter,
patternsasVec<Vec<TileType>>- the type we used to build our patterns. A second parameter,chunk_sizeis the same as we've used before. It returns avectorof the newMapChunktype. AMapChunkis a pattern, but with additional exit and compatibility information added to it. So we're promising that given a set of pattern graphics, we're going to add all the navigation information to it and return the patterns as a set of chunks. - It makes a new
Vecof typeMapChunkcalledconstraints. This is our result - we'll be adding to it, and returning it to the caller at the end. - Now we iterate every pattern in
patterns, calling itp(to save typing). For each pattern:- We make a new
MapChunk. Thepatternfield gets a copy of our pattern.exitsis an array (fixed size set; in this case of size 4) of vectors, so we insert 4 empty vectors into it.compatible_withis also an array of vectors, so we set those to new - empty - vectors. We sethas_exitstotrue- we'll set that later. - We iterate from 0 to
chunk_size, and addfalseinto eachexitsfield of the new map chunk. Theexitsstructure represents one entry per possible direction (North, South, West, East) - so it needs one entry per size of the chunk to represent each possible exit tile in that direction. We'll check for actual connectivity later - for now, we just want placeholders for each direction. - We set
n_exitsto 0, and make it mutable - so we can add to it later. We'll be counting the total number of exits on the way through. - We iterate
xfrom 0 tochunk_size, and for each value ofx:- We check for north-bound exits. These are always at the location
(x, 0)within the chunk - so we calculate the tile index to check astile_idx_in_chunk(chunk_size, x, 0). If that tile is a floor, we add one ton_exitsand setnew_chunk.exits[0][x]totrue. - We do the same for south-bound exits. These are always at the location
(x, chunk_size-1), so we calculate the chunk index to betile_idx_in_chunk(chunk_size, x, chunk_size-1). If that tile is a floor, we add one ton_exitsand setnew_chunks.exits[1][x]totrue. - We do the same again for west-bound, which are at location
(0,x). - We do the same again for east-bound, which are at location
(chunk_size-1,0).
- We check for north-bound exits. These are always at the location
- If
n_exitsis 0, we setnew_chunk.has_exitsto 0 - there's no way in or out of this chunk! - We push
new_chunkto theconstraintsresult vector.
- We make a new
- Now it's time to build a compatibility matrix! The idea here is to match which tiles can be placed to which other tiles, by matching exits on adjacent edges.
- To avoid borrow-checker issues, we take a copy of the existing constraints with
let ch = constraints.clone();. Rust isn't a big fan of both reading from and writing to the samevectorat once - so this avoids us having to do a dance to keep it separated. - For each
constraintin or results vectorconstraints, namedcwe:- Iterate every constraint in
ch, our copy of the constraints vector, aspotential. We add an enumerator,jto tell us how it is indexed.- If neither
c(the constraint we are editing) orpotential(the constraint we are examining) has exits, then we make it compatible with everything. We do this to increase the chances of a map being successfully resolved and still featuring these tiles (otherwise, they would never be chosen). To add compatibility with everything, we addjto thecompatibile_withstructure for all four directions. Soccan be placed next topotentialin any direction. - Otherwise, we iterate through all four exit directions on
c:- We set
oppositeto the reciprocal of the direction we're evaluating; so North goes to South, East to West, etc. - We setup two mutable variables,
it_fitsandhas_any- and set both tofalse. We'll use these in the next steps.it_fitsmeans that there are one or more matching exits betweenc's exit tiles andpotential's entry tiles.has_anymeans thatchas any exits at all in this direction. We distinguish between the two because if there are no exits in that direction, we don't care what the neighbor is - we can't affect it. If there are exits, then we only want to be compatible with tiles you can actually visit. - We iterate
c's exits, keeping both aslot(the tile number we are evaluating) and the value of theexittile (can_enter). You'll remember that we've set these totrueif they are a floor - andfalseotherwise - so we're iterating possible exits.- If
can_enteristrue, then we sethas_anyto true - it has an exit in that direction. - We check
potential_exits.exits[opposite][slot]- that is that matching exit on the other tile, in the opposite direction to the way we're going. If there is a match-up, then you can go from tilecto tilepotentialin our currentdirection! That lets us setit_fitsto true.
- If
- If
it_fitsistrue, then there is a compatibility between the tiles: we addjtoc'scompatible_withvector for the current direction. - If
has_anyisfalse, then we don't care about adjacency in this direction - so we addjto the compatibility matrix for all directions, just like we did for a tile with no exits.
- We set
- If neither
- Iterate every constraint in
- Finally, we return our
constraintsresults vector.
That's quite a complicated algorithm, so we don't really want to trust that I got it right. We'll verify exit detection by adjusting our tile gallery code to show exits. In build, tweak the rendering order and what we're passing to render_tile_gallery:
#![allow(unused)] fn main() { let patterns = build_patterns(&self.map, CHUNK_SIZE, true, true); let constraints = patterns_to_constraints(patterns, CHUNK_SIZE); self.render_tile_gallery(&constraints, CHUNK_SIZE); }
We also need to modify render_tile_gallery:
#![allow(unused)] fn main() { fn render_tile_gallery(&mut self, constraints: &Vec<MapChunk>, chunk_size: i32) { self.map = Map::new(0); let mut counter = 0; let mut x = 1; let mut y = 1; while counter < constraints.len() { render_pattern_to_map(&mut self.map, &constraints[counter], chunk_size, x, y); x += chunk_size + 1; if x + chunk_size > self.map.width { // Move to the next row x = 1; y += chunk_size + 1; if y + chunk_size > self.map.height { // Move to the next page self.take_snapshot(); self.map = Map::new(0); x = 1; y = 1; } } counter += 1; } self.take_snapshot(); } }
This requires that we modify our render_pattern_to_map function, also:
#![allow(unused)] fn main() { pub fn render_pattern_to_map(map : &mut Map, chunk: &MapChunk, chunk_size: i32, start_x : i32, start_y: i32) { let mut i = 0usize; for tile_y in 0..chunk_size { for tile_x in 0..chunk_size { let map_idx = map.xy_idx(start_x + tile_x, start_y + tile_y); map.tiles[map_idx] = chunk.pattern[i]; map.visible_tiles[map_idx] = true; i += 1; } } for (x,northbound) in chunk.exits[0].iter().enumerate() { if *northbound { let map_idx = map.xy_idx(start_x + x as i32, start_y); map.tiles[map_idx] = TileType::DownStairs; } } for (x,southbound) in chunk.exits[1].iter().enumerate() { if *southbound { let map_idx = map.xy_idx(start_x + x as i32, start_y + chunk_size -1); map.tiles[map_idx] = TileType::DownStairs; } } for (x,westbound) in chunk.exits[2].iter().enumerate() { if *westbound { let map_idx = map.xy_idx(start_x, start_y + x as i32); map.tiles[map_idx] = TileType::DownStairs; } } for (x,eastbound) in chunk.exits[3].iter().enumerate() { if *eastbound { let map_idx = map.xy_idx(start_x + chunk_size - 1, start_y + x as i32); map.tiles[map_idx] = TileType::DownStairs; } } } }
Now that we have the demo framework running, we can cargo run the project - and see the tiles from wfc-demo2.xp correctly highlighting the exits:
 .
.
The wfc-demo1.xp exits are also highlighted:
 .
.
That's great! Our exit finder is working correctly.
Building the Solver
Do you remember the old books of logic problems you used to be able to buy for long trips? "Fred is a lawyer, Mary is a doctor, and Jim is unemployed. Fred can't sit next to unemployed people, because he's snooty. Mary likes everyone. How should you arrange their seating?" This is an example of the type of constrained problem a solver is designed to help with. Building our map is no different - we're reading the constraints matrix (which we built above) to determine which tiles we can place in any given area. Because it's a roguelike, and we want something different every time, we want to inject some randomness - and get a different but valid map every time.
Let's extend our build function to call a hypothetical solver:
#![allow(unused)] fn main() { let patterns = build_patterns(&self.map, CHUNK_SIZE, true, true); let constraints = patterns_to_constraints(patterns, CHUNK_SIZE); self.render_tile_gallery(&constraints, CHUNK_SIZE); self.map = Map::new(self.depth); loop { let mut solver = Solver::new(constraints.clone(), CHUNK_SIZE, &self.map); while !solver.iteration(&mut self.map, &mut rng) { self.take_snapshot(); } self.take_snapshot(); if solver.possible { break; } // If it has hit an impossible condition, try again } }
We make a freshly solid map (since we've been using it for rendering tile demos, and don't want to pollute the final map with a demo gallery!). Then we loop (the Rust loop that runs forever until something calls break). Inside that loop, we create a solver for a copy of the constraints matrix (we copy it in case we have to go through repeatedly; otherwise, we'd have to move it in and move it out again). We repeatedly call the solver's iteration function, taking a snapshot each time - until it reports that it is done. If the solver gave up and said it wasn't possible, we try again.
We'll start by adding solver.rs to our waveform_collapse directory. The solver needs to keep its own state: that is, as it iterates through, it needs to know how far it has come. We'll support this by making Solver into a struct:
#![allow(unused)] fn main() { pub struct Solver { constraints: Vec<MapChunk>, chunk_size : i32, chunks : Vec<Option<usize>>, chunks_x : usize, chunks_y : usize, remaining : Vec<(usize, i32)>, // (index, # neighbors) pub possible: bool } }
It stores the constraints we've been building, the chunk_size we're using, the chunks we're resolving (more on that in a second), the number of chunks it can fit onto the target map (chunks_x, and chunks_y), a remaining vector (more on that, too), and a possible indicator to indicate whether or not it gave up.
chunks is a vector of Option<usize>. The usize value is the index of the chunk. It's an option because we may not have filled it in, yet - so it might be None or Some(usize). This nicely represents the "quantum waveform collapse" nature of the problem - it either exists or it doesn't, and we don't know until we look at it!
remaining is a vector of all of the chunks, with their index. It's a tuple - we store the chunk index in the first entry, and the number of existing neighbors in the second. We'll use that to help decide which chunk to fill in next, and remove it from the remaining list when we've added one.
We'll need to implement methods for Solver, too. new is a basic constructor:
#![allow(unused)] fn main() { impl Solver { pub fn new(constraints: Vec<MapChunk>, chunk_size: i32, map : &Map) -> Solver { let chunks_x = (map.width / chunk_size) as usize; let chunks_y = (map.height / chunk_size) as usize; let mut remaining : Vec<(usize, i32)> = Vec::new(); for i in 0..(chunks_x*chunks_y) { remaining.push((i, 0)); } Solver { constraints, chunk_size, chunks: vec![None; chunks_x * chunks_y], chunks_x, chunks_y, remaining, possible: true } } ... }
It calculates the size (for chunks_x and chunks_y), fills remaining with every tile and no neighbors, and chunks with None values. This sets us up for our solving run! We also need a helper function called chunk_idx:
#![allow(unused)] fn main() { fn chunk_idx(&self, x:usize, y:usize) -> usize { ((y * self.chunks_x) + x) as usize } }
This is a lot like xy_idx in map, or tile_idx_in_chunk in common - but is constrained by the number of chunks we can fit onto our map. We'll also rely on count_neighbors:
#![allow(unused)] fn main() { fn count_neighbors(&self, chunk_x:usize, chunk_y:usize) -> i32 { let mut neighbors = 0; if chunk_x > 0 { let left_idx = self.chunk_idx(chunk_x-1, chunk_y); match self.chunks[left_idx] { None => {} Some(_) => { neighbors += 1; } } } if chunk_x < self.chunks_x-1 { let right_idx = self.chunk_idx(chunk_x+1, chunk_y); match self.chunks[right_idx] { None => {} Some(_) => { neighbors += 1; } } } if chunk_y > 0 { let up_idx = self.chunk_idx(chunk_x, chunk_y-1); match self.chunks[up_idx] { None => {} Some(_) => { neighbors += 1; } } } if chunk_y < self.chunks_y-1 { let down_idx = self.chunk_idx(chunk_x, chunk_y+1); match self.chunks[down_idx] { None => {} Some(_) => { neighbors += 1; } } } neighbors } }
This function could be a lot smaller, but I've left it spelling out every step for clarity. It looks at a chunk, and determines if it has a created (not set to None) chunk to the North, South, East and West.
Finally, we get to the iteration function - which does the hard work:
#![allow(unused)] fn main() { pub fn iteration(&mut self, map: &mut Map, rng : &mut super::RandomNumberGenerator) -> bool { if self.remaining.is_empty() { return true; } // Populate the neighbor count of the remaining list let mut remain_copy = self.remaining.clone(); let mut neighbors_exist = false; for r in remain_copy.iter_mut() { let idx = r.0; let chunk_x = idx % self.chunks_x; let chunk_y = idx / self.chunks_x; let neighbor_count = self.count_neighbors(chunk_x, chunk_y); if neighbor_count > 0 { neighbors_exist = true; } *r = (r.0, neighbor_count); } remain_copy.sort_by(|a,b| b.1.cmp(&a.1)); self.remaining = remain_copy; // Pick a random chunk we haven't dealt with yet and get its index, remove from remaining list let remaining_index = if !neighbors_exist { (rng.roll_dice(1, self.remaining.len() as i32)-1) as usize } else { 0usize }; let chunk_index = self.remaining[remaining_index].0; self.remaining.remove(remaining_index); let chunk_x = chunk_index % self.chunks_x; let chunk_y = chunk_index / self.chunks_x; let mut neighbors = 0; let mut options : Vec<Vec<usize>> = Vec::new(); if chunk_x > 0 { let left_idx = self.chunk_idx(chunk_x-1, chunk_y); match self.chunks[left_idx] { None => {} Some(nt) => { neighbors += 1; options.push(self.constraints[nt].compatible_with[3].clone()); } } } if chunk_x < self.chunks_x-1 { let right_idx = self.chunk_idx(chunk_x+1, chunk_y); match self.chunks[right_idx] { None => {} Some(nt) => { neighbors += 1; options.push(self.constraints[nt].compatible_with[2].clone()); } } } if chunk_y > 0 { let up_idx = self.chunk_idx(chunk_x, chunk_y-1); match self.chunks[up_idx] { None => {} Some(nt) => { neighbors += 1; options.push(self.constraints[nt].compatible_with[1].clone()); } } } if chunk_y < self.chunks_y-1 { let down_idx = self.chunk_idx(chunk_x, chunk_y+1); match self.chunks[down_idx] { None => {} Some(nt) => { neighbors += 1; options.push(self.constraints[nt].compatible_with[0].clone()); } } } if neighbors == 0 { // There is nothing nearby, so we can have anything! let new_chunk_idx = (rng.roll_dice(1, self.constraints.len() as i32)-1) as usize; self.chunks[chunk_index] = Some(new_chunk_idx); let left_x = chunk_x as i32 * self.chunk_size as i32; let right_x = (chunk_x as i32+1) * self.chunk_size as i32; let top_y = chunk_y as i32 * self.chunk_size as i32; let bottom_y = (chunk_y as i32+1) * self.chunk_size as i32; let mut i : usize = 0; for y in top_y .. bottom_y { for x in left_x .. right_x { let mapidx = map.xy_idx(x, y); let tile = self.constraints[new_chunk_idx].pattern[i]; map.tiles[mapidx] = tile; i += 1; } } } else { // There are neighbors, so we try to be compatible with them let mut options_to_check : HashSet<usize> = HashSet::new(); for o in options.iter() { for i in o.iter() { options_to_check.insert(*i); } } let mut possible_options : Vec<usize> = Vec::new(); for new_chunk_idx in options_to_check.iter() { let mut possible = true; for o in options.iter() { if !o.contains(new_chunk_idx) { possible = false; } } if possible { possible_options.push(*new_chunk_idx); } } if possible_options.is_empty() { rltk::console::log("Oh no! It's not possible!"); self.possible = false; return true; } else { let new_chunk_idx = if possible_options.len() == 1 { 0 } else { rng.roll_dice(1, possible_options.len() as i32)-1 }; self.chunks[chunk_index] = Some(new_chunk_idx as usize); let left_x = chunk_x as i32 * self.chunk_size as i32; let right_x = (chunk_x as i32+1) * self.chunk_size as i32; let top_y = chunk_y as i32 * self.chunk_size as i32; let bottom_y = (chunk_y as i32+1) * self.chunk_size as i32; let mut i : usize = 0; for y in top_y .. bottom_y { for x in left_x .. right_x { let mapidx = map.xy_idx(x, y); let tile = self.constraints[new_chunk_idx as usize].pattern[i]; map.tiles[mapidx] = tile; i += 1; } } } } false } }
This is another really big function, but once again that's because I tried to keep it easy to read. Let's walk through the algorithm:
- If there is nothing left in
remaining, we return that we have completed the map.possibleis true, because we actually finished the problem. - We take a
cloneofremainingto avoid borrow checker issues. - We iterate our copy of
remaining, and for each remaining chunk:- We determine it's
xandylocation from the chunk index. - We call
count_neighborsto determine how many (if any) neighboring chunks have been resolved. - If any neighbors were found, we set
neighbors_existto true - telling the algorithm that it has run at least once. - We update the copy of the
remaininglist to include the same index as before, and the new neighbor count.
- We determine it's
- We sort our copy of
remainingby the number of neighbors, descending - so the chunk with the most neighbors is first. - We copy our clone of
remainingback to our actualremaininglist. - We want to create a new variable,
remaining_index- to indicate which chunk we're going to work on, and where it is in theremainingvector. If we haven't made any tiles yet, we pick our starting point at random. Otherwise, we pick the first entry in theremaininglist - which will be the one with the most neighbors. - We obtain
chunk_idxfrom theremaining listat the selected index, and remove that chunk from the list. - Now we calculate
chunk_xandchunk_yto tell us where it is on the new map. - We set a mutable variable,
neighborsto 0; we'll be counting neighbors again. - We create a mutable variable called
Options. It has the rather strange typeVec<Vec<usize>>- it is a vector of vectors, each of which contains an array index (usize). We'll be storing compatible options for each direction in here - so we need the outer vector for directions, and the inner vector for options. These index theconstraintsvector. - If it isn't the left-most chunk on the map, it may have a chunk to the west - so we calculate the index of that chunk. If a chunk to the west exists (isn't
None), then we add it's east boundcompatible_withlist to ourOptionsvector. We incrementneighborsto indicate that we found a neighbor. - We repeat for the east - if it isn't the right-most chunk on the map. We increment
neighborsto indicate that we found a neighbor. - We repeat for the south - if it isn't the bottom chunk on the map. We increment
neighborsto indicate that we found a neighbor. - We repeat for the north - if it isn't the top chunk on the map. We increment
neighborsto indicate that we found a neighbor. - If there are no neighbors, we:
- Find a random tile from
constraints. - Figure out the bounds of where we are placing the tile in
left_x,right_x,top_y, andbottom_y. - Copy the selected tile to the map.
- Find a random tile from
- If there are neighbors, we:
- Insert all of the options from each direction into a
HashSet. We usedHashSetto de-duplicate our tiles earlier, and this is what we're doing here: we're removing all duplicate options, so we don't evaluate them repeatedly. - We make a new vector called
possible_options. For each option in theHashSet:- Set a mutable variable called
possibletotrue. - Check each directions'
options, and if it is compatible with its neighbors preferences - add it topossible_options.
- Set a mutable variable called
- If
possible_optionsis empty - then we've hit a brick wall, and can't add any more tiles. We setpossibleto false in the parent structure and bail out! - Otherwise, we pick a random entry from
possible_optionsand draw it to the map.
- Insert all of the options from each direction into a
So while it's a long function, it isn't a really complicated one. It looks for possible combinations for each iteration, and tries to apply them - giving up and returning failure if it can't find one.
The caller is already taking snapshots of each iteration, so if we cargo run the project with our wfc-test1.xp file we get something like this:
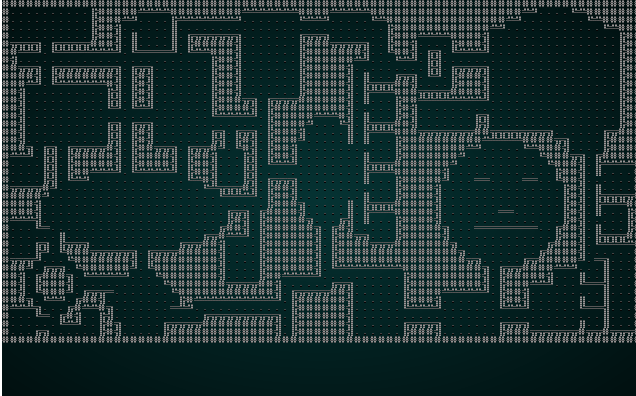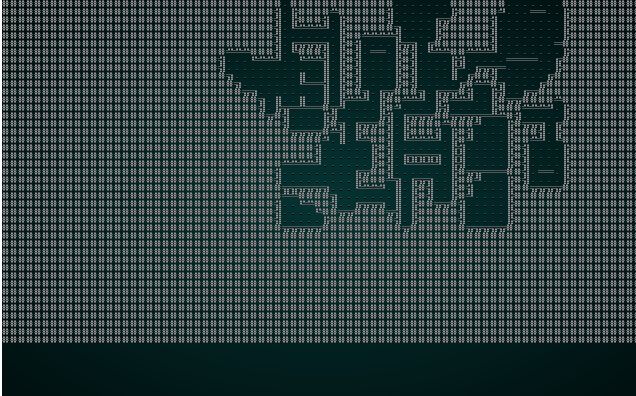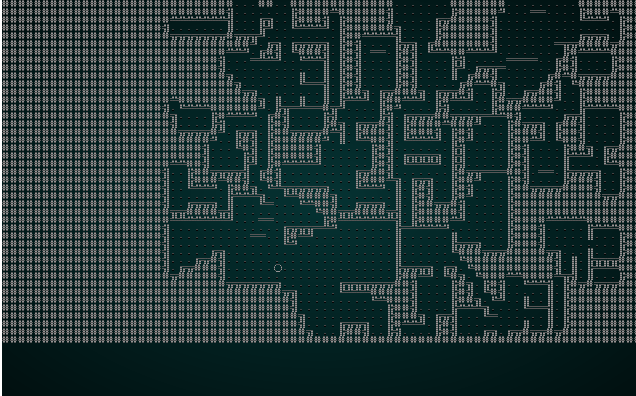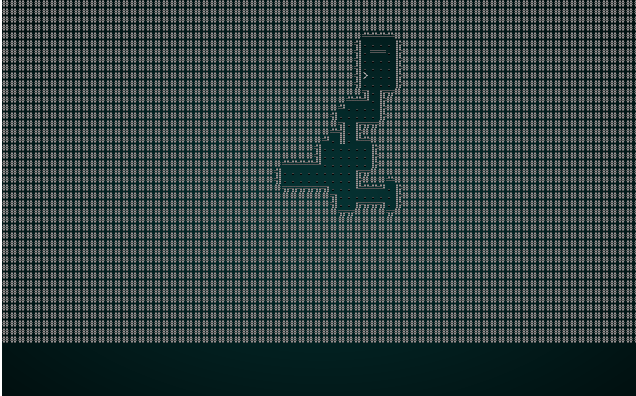 .
.
Not the greatest map, but you can watch the solver chug along - placing tiles one at a time. Now lets try it with wfc-test2.xmp, a set of tiles designed for tiling:
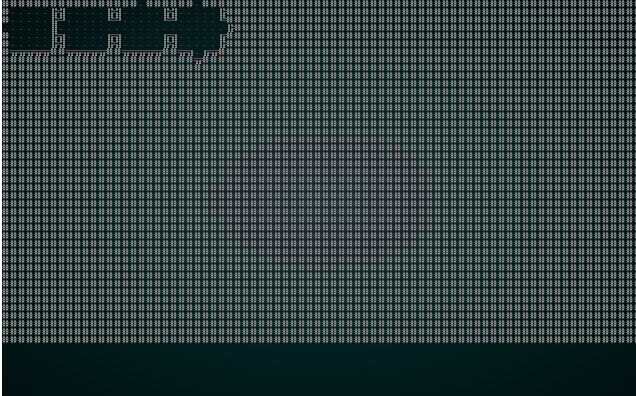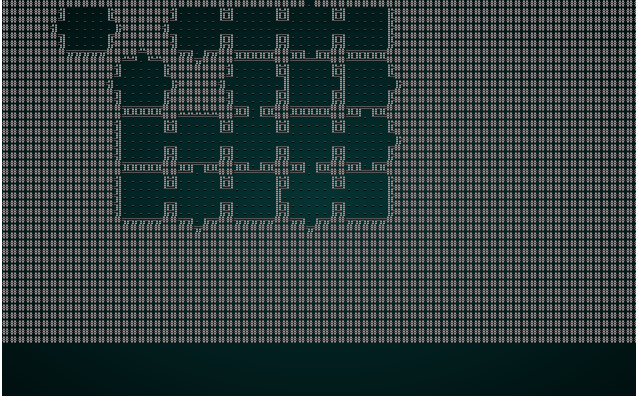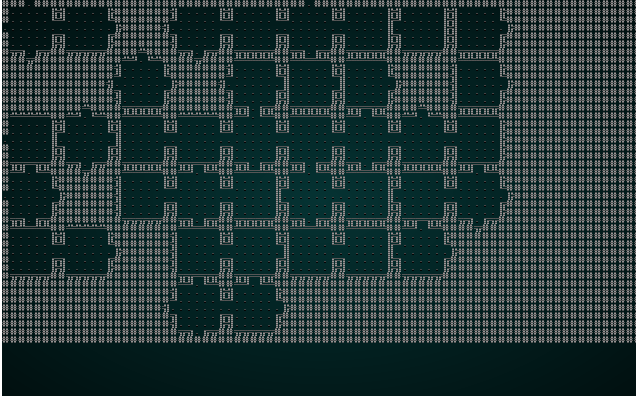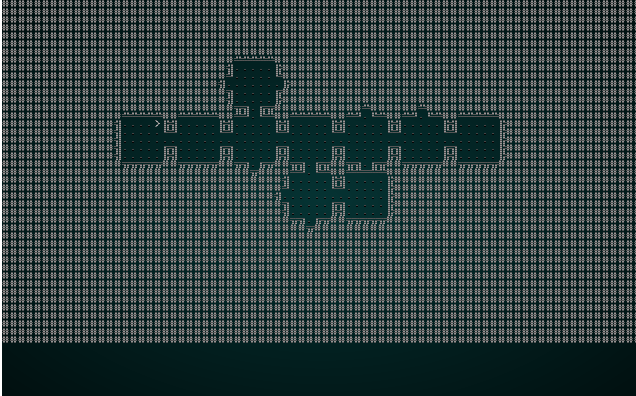 .
.
This is kind-of fun - it lays it out like a jigsaw, and eventually gets a map! The map isn't as well connected as one might hope, the edges with no exit lead to a smaller play area (which is culled at the end). It's still a good start!
Reducing the chunk size
We can significantly improve the resulting map in this case by reducing our CHUNK_SIZE constant to 3. Running it with test map 1 produces something like this:
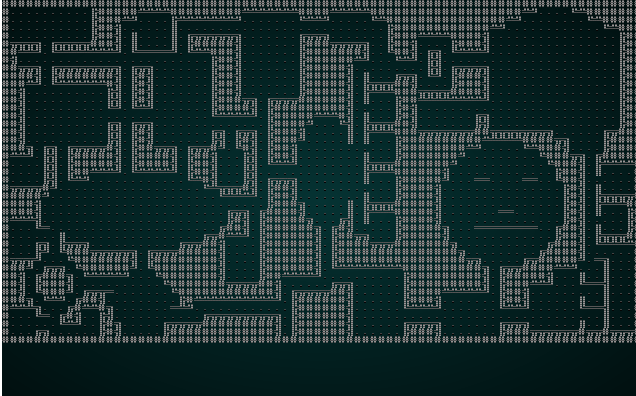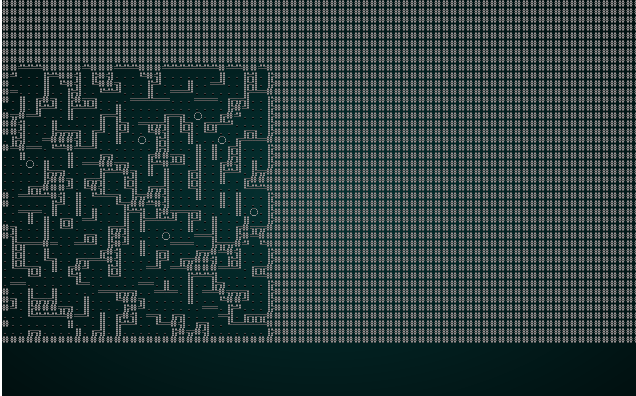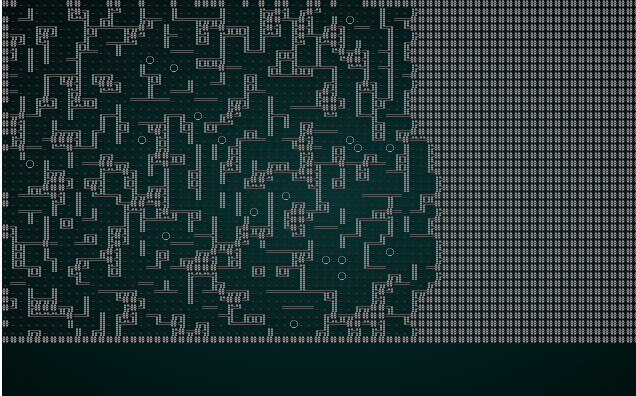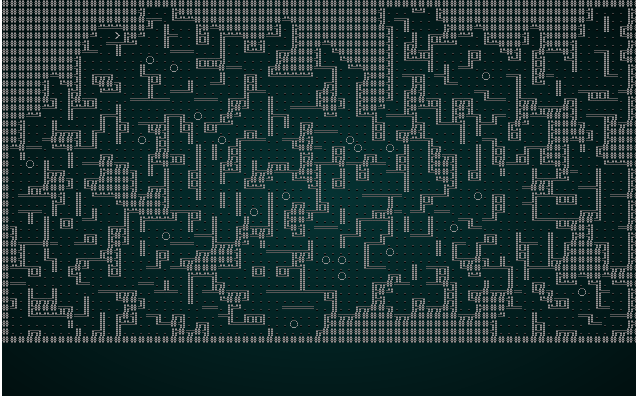 .
.
That's a much more interesting map! You can try it with wfc-test2.xp as well:
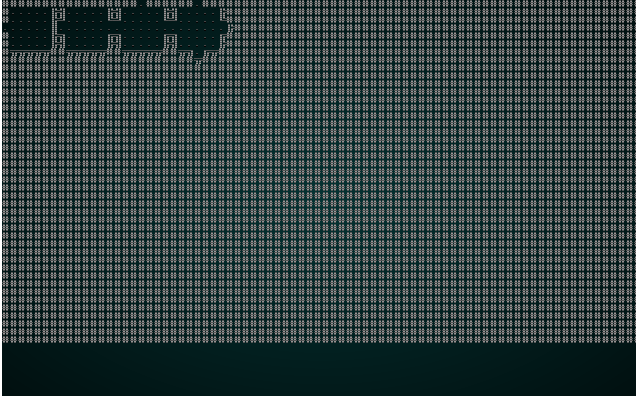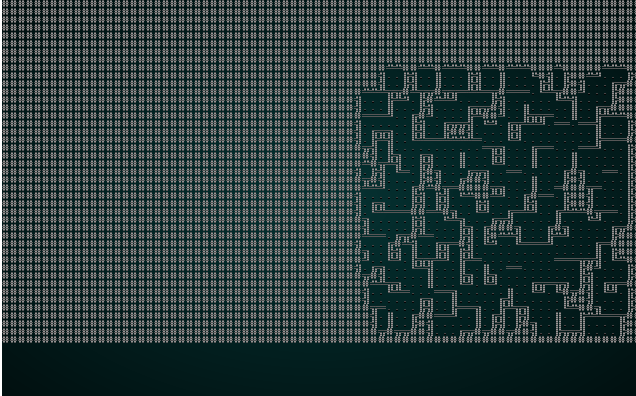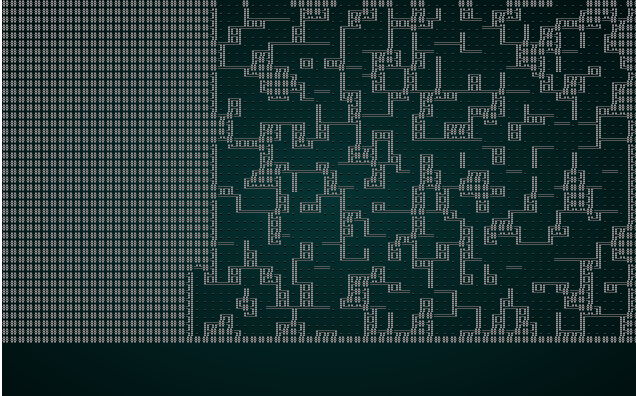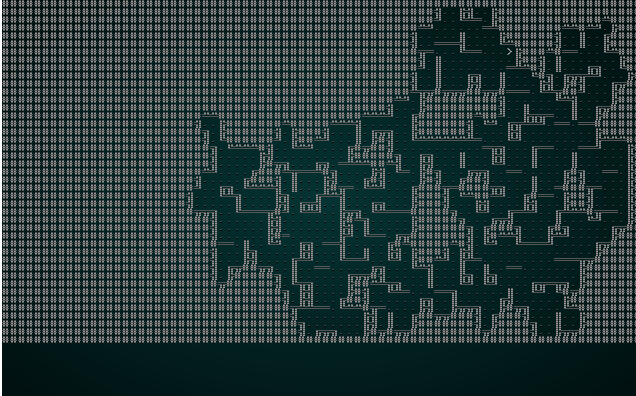 .
.
Once again, it's an interesting and playable map! The problem is that we've got such a small chunk size that there really aren't all that many interesting options for adjacency - 3x3 grids really limits the amount of variability you can have on your map! So we'll try wfc-test1.xp with a chunk size of 5:
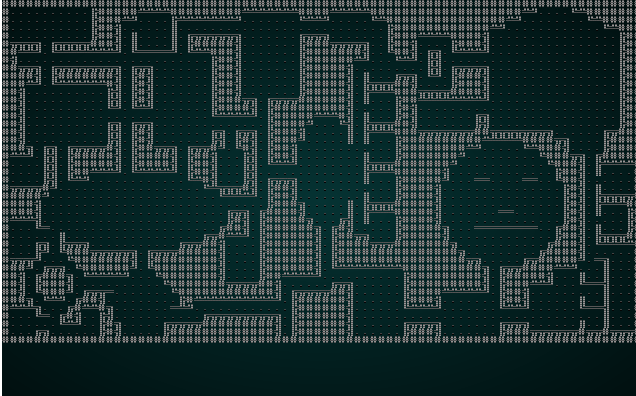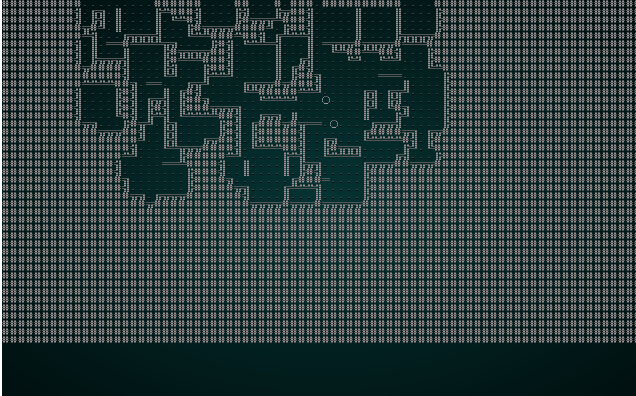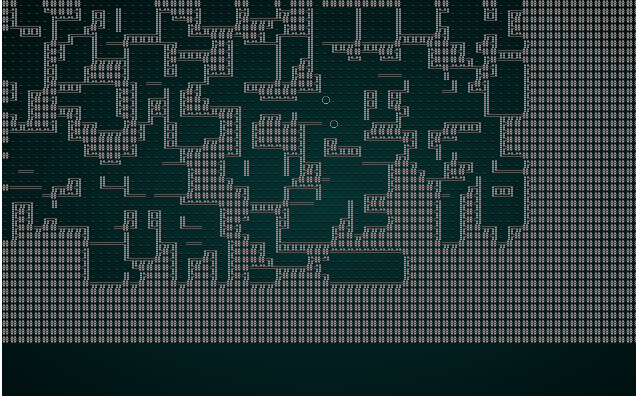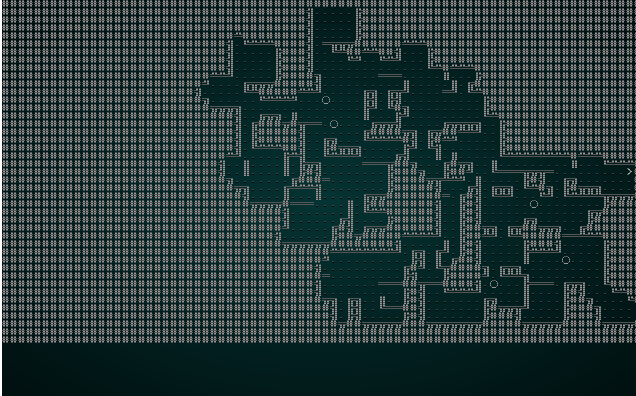 .
.
That's more like it! It's not dissimilar from a map we might try and generate in another fashion.
Taking advantage of the ability to read other map types
Rather than loading one of our .xp files, lets feed in the results of a CellularAutomata run, and use that as the seed with a large (8) chunk. This is surprisingly easy with the structure we have! In our build function:
#![allow(unused)] fn main() { const CHUNK_SIZE :i32 = 8; let mut ca = super::CellularAutomataBuilder::new(0); ca.build_map(); self.map = ca.get_map(); for t in self.map.tiles.iter_mut() { if *t == TileType::DownStairs { *t = TileType::Floor; } } }
Notice that we're removing down stairs - the Cellular Automata generator will place one, and we don't want stairs everywhere! This gives a very pleasing result:
 .
.
Improving adjacency - and increasing the risk of rejection!
What we have already is quite a workable solution - you can make decent maps with it, especially when you use other generators as the seed. On winding jigsaw maps, it's not generating the adjacency we'd like. There's a small risk by making the matcher more specific that we will see some failures, but lets give it a go anyway. In our code that builds a compatibility matrix, find the comment There's no exits on this side and replace the section with this code:
#![allow(unused)] fn main() { if !has_any { // There's no exits on this side, let's match only if // the other edge also has no exits let matching_exit_count = potential.exits[opposite].iter().filter(|a| !**a).count(); if matching_exit_count == 0 { c.compatible_with[direction].push(j); } } }
Run against the our cellular automata example, we see a bit of a change:
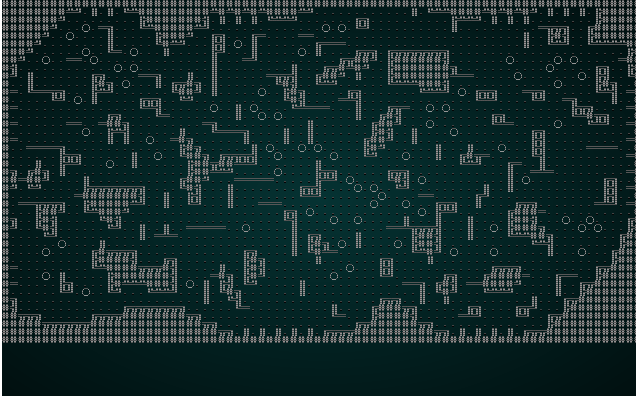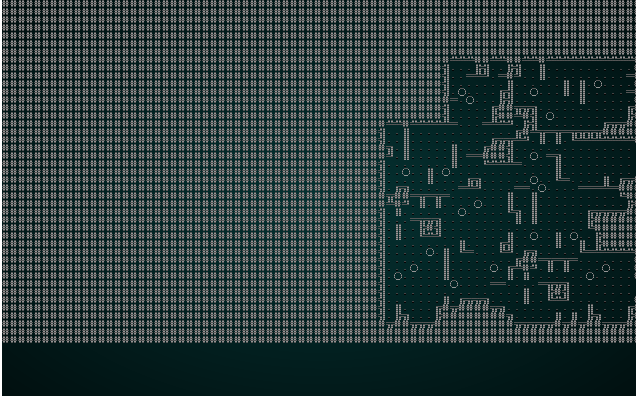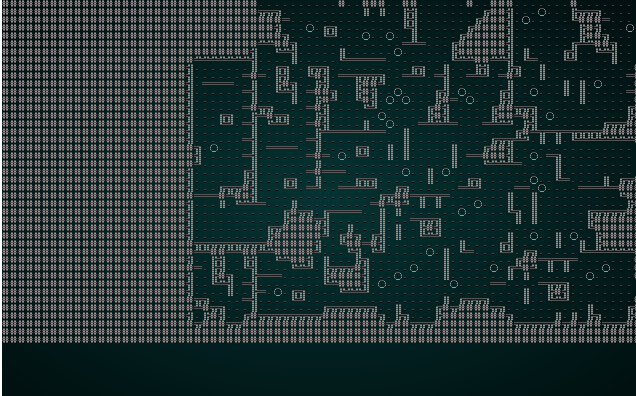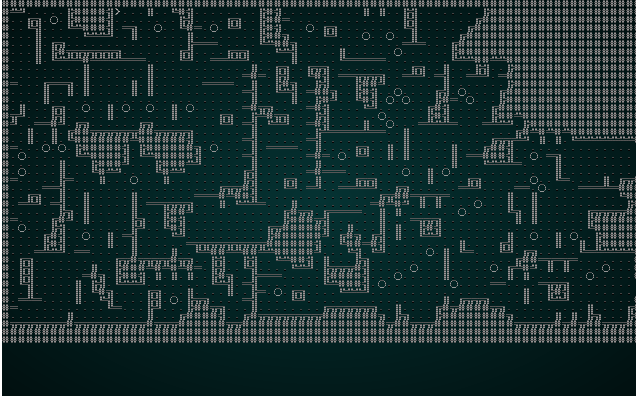 .
.
It also looks pretty good with our map test 1:
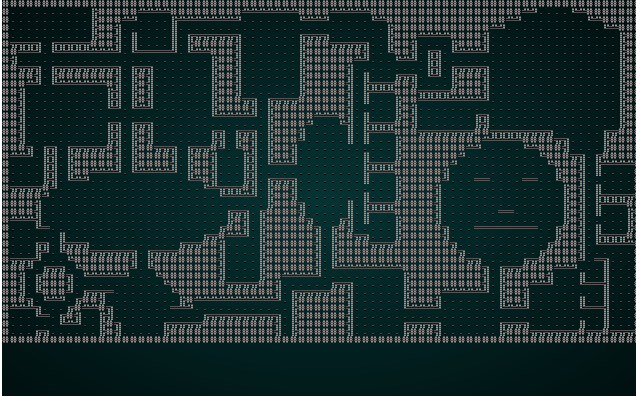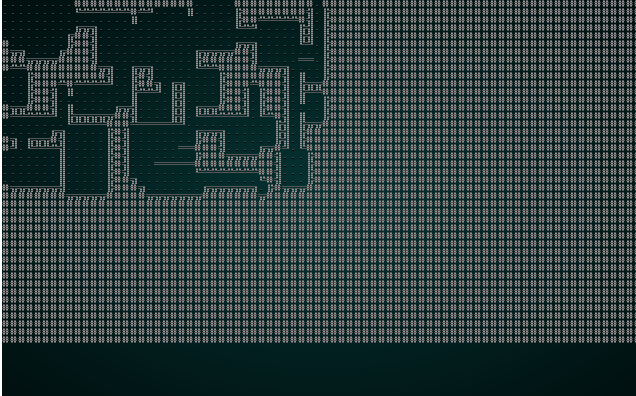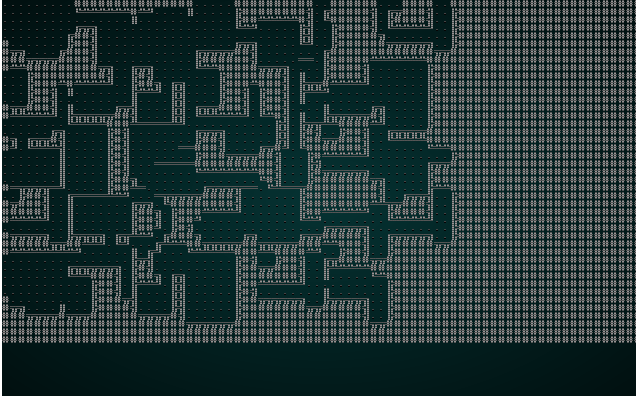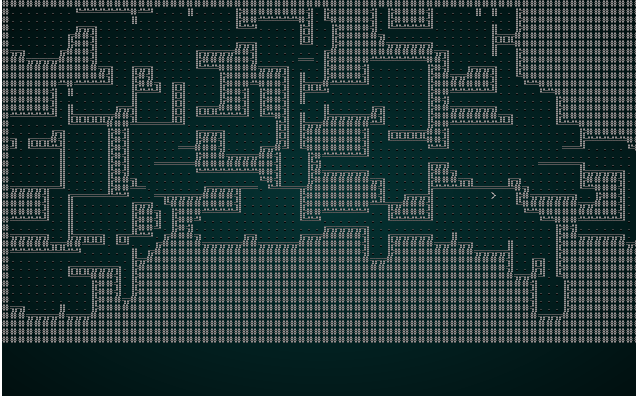 .
.
Overall, that change is a winner! It doesn't look very good with our jigsaw puzzle anymore; there just aren't enough tiles to make good patterns.
Offering different build options to the game
We're going to offer three modes to our random_builder function: TestMap (just the REX Paint map), and Derived (run on an existing algorithm). So, in mod.rs we add an enumeration and extend our structure to hold some related data:
#![allow(unused)] fn main() { #[derive(PartialEq, Copy, Clone)] pub enum WaveformMode { TestMap, Derived } pub struct WaveformCollapseBuilder { map : Map, starting_position : Position, depth: i32, history: Vec<Map>, noise_areas : HashMap<i32, Vec<usize>>, mode : WaveformMode, derive_from : Option<Box<dyn MapBuilder>> } }
We'll extend our new constructor to include these:
#![allow(unused)] fn main() { impl WaveformCollapseBuilder { pub fn new(new_depth : i32, mode : WaveformMode, derive_from : Option<Box<dyn MapBuilder>>) -> WaveformCollapseBuilder { WaveformCollapseBuilder{ map : Map::new(new_depth), starting_position : Position{ x: 0, y : 0 }, depth : new_depth, history: Vec::new(), noise_areas : HashMap::new(), mode, derive_from } } }
Then we'll add some functionality into the top of our build function:
#![allow(unused)] fn main() { fn build(&mut self) { if self.mode == WaveformMode::TestMap { self.map = load_rex_map(self.depth, &rltk::rex::XpFile::from_resource("../../resources/wfc-demo1.xp").unwrap()); self.take_snapshot(); return; } let mut rng = RandomNumberGenerator::new(); const CHUNK_SIZE :i32 = 8; let prebuilder = &mut self.derive_from.as_mut().unwrap(); prebuilder.build_map(); self.map = prebuilder.get_map(); for t in self.map.tiles.iter_mut() { if *t == TileType::DownStairs { *t = TileType::Floor; } } self.take_snapshot(); ... }
Now we'll add a couple of constructors to make it easier for random_builder to not have to know about the innards of the WFC algorithm:
#![allow(unused)] fn main() { pub fn test_map(new_depth: i32) -> WaveformCollapseBuilder { WaveformCollapseBuilder::new(new_depth, WaveformMode::TestMap, None) } pub fn derived_map(new_depth: i32, builder: Box<dyn MapBuilder>) -> WaveformCollapseBuilder { WaveformCollapseBuilder::new(new_depth, WaveformMode::Derived, Some(builder)) } }
Lastly, we'll modify our random_builder (in map_builders/mod.rs) to sometimes return the test map - and sometimes run WFC on whatever map we've created:
#![allow(unused)] fn main() { pub fn random_builder(new_depth: i32) -> Box<dyn MapBuilder> { let mut rng = rltk::RandomNumberGenerator::new(); let builder = rng.roll_dice(1, 17); let mut result : Box<dyn MapBuilder>; match builder { 1 => { result = Box::new(BspDungeonBuilder::new(new_depth)); } 2 => { result = Box::new(BspInteriorBuilder::new(new_depth)); } 3 => { result = Box::new(CellularAutomataBuilder::new(new_depth)); } 4 => { result = Box::new(DrunkardsWalkBuilder::open_area(new_depth)); } 5 => { result = Box::new(DrunkardsWalkBuilder::open_halls(new_depth)); } 6 => { result = Box::new(DrunkardsWalkBuilder::winding_passages(new_depth)); } 7 => { result = Box::new(DrunkardsWalkBuilder::fat_passages(new_depth)); } 8 => { result = Box::new(DrunkardsWalkBuilder::fearful_symmetry(new_depth)); } 9 => { result = Box::new(MazeBuilder::new(new_depth)); } 10 => { result = Box::new(DLABuilder::walk_inwards(new_depth)); } 11 => { result = Box::new(DLABuilder::walk_outwards(new_depth)); } 12 => { result = Box::new(DLABuilder::central_attractor(new_depth)); } 13 => { result = Box::new(DLABuilder::insectoid(new_depth)); } 14 => { result = Box::new(VoronoiCellBuilder::pythagoras(new_depth)); } 15 => { result = Box::new(VoronoiCellBuilder::manhattan(new_depth)); } 16 => { result = Box::new(WaveformCollapseBuilder::test_map(new_depth)); } _ => { result = Box::new(SimpleMapBuilder::new(new_depth)); } } if rng.roll_dice(1, 3)==1 { result = Box::new(WaveformCollapseBuilder::derived_map(new_depth, result)); } result } }
That's quite a change. We roll a 17-sided dice (wouldn't it be nice if those really existed?), and pick a builder - as before, but with the option to use the .xp file from wfc_test1.xp. We store it in result. Then we roll 1d3; if it comes up 1, we wrap the builder in the WaveformCollapseBuilder in derived mode - so it will take the original map and rebuild it with WFC. Effectively, we just added another 17 options!
Cleaning Up Dead Code Warnings
Let's take a moment to do a little housekeeping on our code.
There are quite a few warnings in the project when you compile. They are almost all "this function is never used" (or equivalent). Since we're building a library of map builders, it's ok to not always call the constructors. You can add an annotation above a function definition - #[allow(dead_code)] to tell the compiler to stop worrying about this. For example, in drunkard.rs:
#![allow(unused)] fn main() { impl DrunkardsWalkBuilder { #[allow(dead_code)] pub fn new(new_depth : i32, settings: DrunkardSettings) -> DrunkardsWalkBuilder { }
I've gone through and applied these where necessary in the example code to silence the compiler.
Cleaning Up Unused Embedded Files
We're not using wfc-test2.xp anymore, so lets remove it from rex-assets.rs:
#![allow(unused)] fn main() { use rltk::{rex::XpFile}; rltk::embedded_resource!(SMALL_DUNGEON, "../../resources/SmallDungeon_80x50.xp"); rltk::embedded_resource!(WFC_DEMO_IMAGE1, "../../resources/wfc-demo1.xp"); pub struct RexAssets { pub menu : XpFile } impl RexAssets { #[allow(clippy::new_without_default)] pub fn new() -> RexAssets { rltk::link_resource!(SMALL_DUNGEON, "../../resources/SmallDungeon_80x50.xp"); rltk::link_resource!(WFC_DEMO_IMAGE1, "../../resources/wfc-demo1.xp"); RexAssets{ menu : XpFile::from_resource("../../resources/SmallDungeon_80x50.xp").unwrap() } } } }
This saves a little bit of space in the resulting binary (never a bad thing: smaller binaries fit into your CPU's cache better, and generally run faster).
The source code for this chapter may be found here
Run this chapter's example with web assembly, in your browser (WebGL2 required)
Copyright (C) 2019, Herbert Wolverson.
