BSP Room Dungeons
About this tutorial
This tutorial is free and open source, and all code uses the MIT license - so you are free to do with it as you like. My hope is that you will enjoy the tutorial, and make great games!
If you enjoy this and would like me to keep writing, please consider supporting my Patreon.
A popular method of map generation uses "binary space partition" to sub-divide your map into rectangles of varying size, and then link the resulting rooms together into corridors. You can go a long way with this method: Nethack uses it extensively, Dungeon Crawl: Stone Soup uses it sometimes, and my project - One Knight in the Dungeon - uses it for sewer levels. This chapter will use the visualizer from the previous chapter to walk you through using this technique.
Implementing a new map - subdivided BSP, the boilerplate
We'll start by making a new file in map_builders - bsp_dungeon.rs. We start by making the basic BspDungeonBuilder struct:
#![allow(unused)] fn main() { pub struct BspDungeonBuilder { map : Map, starting_position : Position, depth: i32, rooms: Vec<Rect>, history: Vec<Map>, rects: Vec<Rect> } }
This is basically the same as the one from SimpleMapBuilder - and we've kept the rooms vector, because this method uses a concept of rooms as well. We've added a rects vector: the algorithm uses this a lot, so it's helpful to make it available throughout the implementation. We'll see why it's needed shortly.
Now we implement the MapBuilder trait to the type:
#![allow(unused)] fn main() { impl MapBuilder for BspDungeonBuilder { fn get_map(&self) -> Map { self.map.clone() } fn get_starting_position(&self) -> Position { self.starting_position.clone() } fn get_snapshot_history(&self) -> Vec<Map> { self.history.clone() } fn build_map(&mut self) { // We should do something here } fn spawn_entities(&mut self, ecs : &mut World) { for room in self.rooms.iter().skip(1) { spawner::spawn_room(ecs, room, self.depth); } } fn take_snapshot(&mut self) { if SHOW_MAPGEN_VISUALIZER { let mut snapshot = self.map.clone(); for v in snapshot.revealed_tiles.iter_mut() { *v = true; } self.history.push(snapshot); } } } }
This is also pretty much the same as SimpleMapBuilder, but build_map has a comment reminding us to write some code. If you ran the generator right now, you'd get a solid blob of walls - and no content whatsoever.
We also need to implement a constructor for BspMapBuilder. Once again, it's basically the same as SimpleMapBuilder:
#![allow(unused)] fn main() { impl BspDungeonBuilder { pub fn new(new_depth : i32) -> BspDungeonBuilder { BspDungeonBuilder{ map : Map::new(new_depth), starting_position : Position{ x: 0, y : 0 }, depth : new_depth, rooms: Vec::new(), history: Vec::new(), rects: Vec::new() } } } }
Lastly, we'll open map_builders/mod.rs and change the random_builder function to always return our new map type:
#![allow(unused)] fn main() { pub fn random_builder(new_depth: i32) -> Box<dyn MapBuilder> { // Note that until we have a second map type, this isn't even slighlty random Box::new(BspDungeonBuilder::new(new_depth)) } }
Once again, this isn't in the slightest bit random - but it's far easier to develop a feature that always runs, rather than keeping trying until it picks the one we want to debug!
Building the map creator
We'll worry about swapping out map types later. Onto making the map! Note that this implementation is ported from my C++ game, One Knight in the Dungeon. We'll start with room generation. Inside our impl BspMapBuilder, we add a new function:
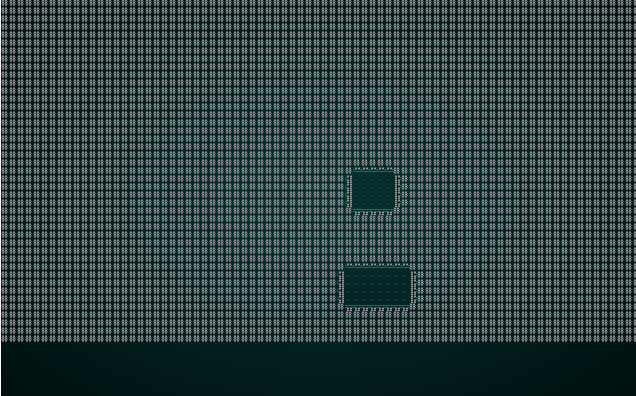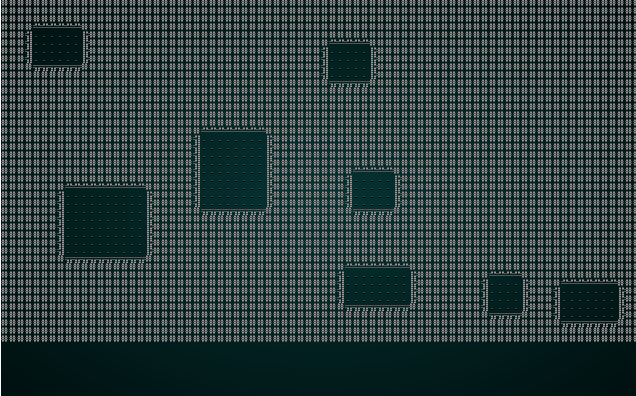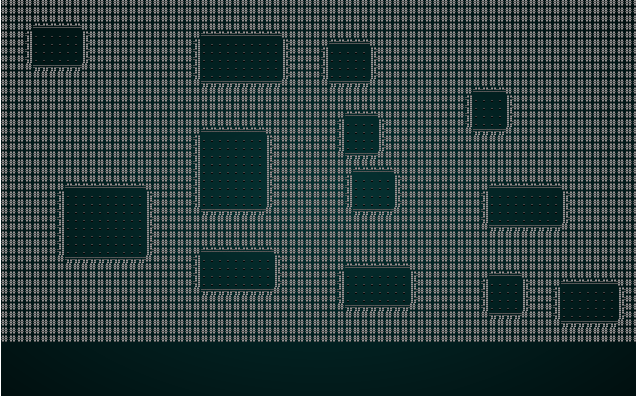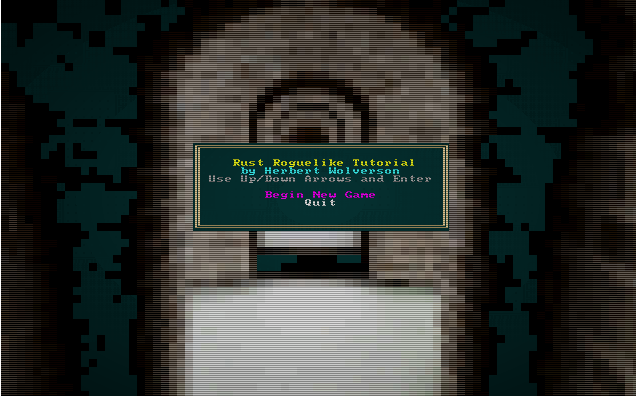
#![allow(unused)] fn main() { fn build(&mut self) { let mut rng = RandomNumberGenerator::new(); self.rects.clear(); self.rects.push( Rect::new(2, 2, self.map.width-5, self.map.height-5) ); // Start with a single map-sized rectangle let first_room = self.rects[0]; self.add_subrects(first_room); // Divide the first room // Up to 240 times, we get a random rectangle and divide it. If its possible to squeeze a // room in there, we place it and add it to the rooms list. let mut n_rooms = 0; while n_rooms < 240 { let rect = self.get_random_rect(&mut rng); let candidate = self.get_random_sub_rect(rect, &mut rng); if self.is_possible(candidate) { apply_room_to_map(&mut self.map, &candidate); self.rooms.push(candidate); self.add_subrects(rect); self.take_snapshot(); } n_rooms += 1; } let start = self.rooms[0].center(); self.starting_position = Position{ x: start.0, y: start.1 }; } }
So what on Earth does this do?
- We clear the
rectsstructure we created as part of the builder. This will be used to store rectangles derived from the overall map. - We create the "first room" - which is really the whole map. We've trimmed a bit to add some padding to the sides of the map.
- We call
add_subrects, passing it the rectangle list - and the first room. We'll implement that in a minute, but what it does is: it divides the rectangle into four quadrants, and adds each of the quadrants to the rectangle list. - Now we setup a room counter, so we don't infinitely loop.
- While that counter is less than 240 (a relatively arbitrary limit that gives fun results):
- We call
get_random_rectto retrieve a random rectangle from the rectangles list. - We call
get_random_sub_rectusing this rectangle as an outer boundary. It creates a random room from 3 to 10 tiles in size (on each axis), somewhere within the parent rectangle. - We ask
is_possibleif the candidate can be drawn to the map; every tile must be within the map boundaries, and not already a room. If it IS possible:- We mark it on the map.
- We add it to the rooms list.
- We call
add_subrectsto sub-divide the rectangle we just used (not the candidate!).
- We call
There's quite a few support functions in play here, so lets go through them.
#![allow(unused)] fn main() { fn add_subrects(&mut self, rect : Rect) { let width = i32::abs(rect.x1 - rect.x2); let height = i32::abs(rect.y1 - rect.y2); let half_width = i32::max(width / 2, 1); let half_height = i32::max(height / 2, 1); self.rects.push(Rect::new( rect.x1, rect.y1, half_width, half_height )); self.rects.push(Rect::new( rect.x1, rect.y1 + half_height, half_width, half_height )); self.rects.push(Rect::new( rect.x1 + half_width, rect.y1, half_width, half_height )); self.rects.push(Rect::new( rect.x1 + half_width, rect.y1 + half_height, half_width, half_height )); } }
The function add_subrects is core to the BSP (Binary Space Partition) approach: it takes a rectangle, and divides the width and height in half. It then creates four new rectangles, one for each quadrant of the original. These are added to the rects list. Graphically:
############### ###############
# # # 1 + 2 #
# # # + #
# 0 # -> #+++++++++++++#
# # # 3 + 4 #
# # # + #
############### ###############
Next up is get_random_rect:
#![allow(unused)] fn main() { fn get_random_rect(&mut self, rng : &mut RandomNumberGenerator) -> Rect { if self.rects.len() == 1 { return self.rects[0]; } let idx = (rng.roll_dice(1, self.rects.len() as i32)-1) as usize; self.rects[idx] } }
This is a simple function. If there is only one rectangle in the rects list, it returns the first one. Otherwise, it rolls a dice for of 1d(size of rects list) and returns the rectangle found at the random index.
Next up is get_random_sub_rect:
#![allow(unused)] fn main() { fn get_random_sub_rect(&self, rect : Rect, rng : &mut RandomNumberGenerator) -> Rect { let mut result = rect; let rect_width = i32::abs(rect.x1 - rect.x2); let rect_height = i32::abs(rect.y1 - rect.y2); let w = i32::max(3, rng.roll_dice(1, i32::min(rect_width, 10))-1) + 1; let h = i32::max(3, rng.roll_dice(1, i32::min(rect_height, 10))-1) + 1; result.x1 += rng.roll_dice(1, 6)-1; result.y1 += rng.roll_dice(1, 6)-1; result.x2 = result.x1 + w; result.y2 = result.y1 + h; result } }
So this takes a rectangle as the parameter, and makes a mutable copy to use as the result. It calculates the width and height of the rectangle, and then produces a random width and height inside that rectangle - but no less than 3 tiles in size and no more than 10 on each dimension. You can tweak those numbers to change your desired room size. It then shunts the rectangle a bit, to provide some random placement (otherwise, it would always be against the sides of the sub-rectangle). Finally, it returns the result. Graphically:
############### ########
# # # 1 #
# # # #
# 0 # -> ########
# #
# #
###############
Finally, the is_possible function:
#![allow(unused)] fn main() { fn is_possible(&self, rect : Rect) -> bool { let mut expanded = rect; expanded.x1 -= 2; expanded.x2 += 2; expanded.y1 -= 2; expanded.y2 += 2; let mut can_build = true; for y in expanded.y1 ..= expanded.y2 { for x in expanded.x1 ..= expanded.x2 { if x > self.map.width-2 { can_build = false; } if y > self.map.height-2 { can_build = false; } if x < 1 { can_build = false; } if y < 1 { can_build = false; } if can_build { let idx = self.map.xy_idx(x, y); if self.map.tiles[idx] != TileType::Wall { can_build = false; } } } } can_build } }
This is a little more complicated, but makes sense when you break it down:
- Take a rectangle as a target, representing the room we are looking at.
- Create a mutable copy of the rectangle called
expanded. We then expand the rectangle out by 2 tiles in each direction, to prevent rooms from overlapping. - We iterate every
xandycoordinate in the rectangle:- If
xoryare out of the map boundaries, we markcan_buildasfalse- this won't work. - If we still can build it, we look at the existing map - if it isn't a solid wall, then we've overlapped an existing room, and mark that we can't build.
- If
- We return the result of
can_build.
So now that we've implemented all of these, the overall algorithm is more obvious:
- We start with a single rectangle covering the entire map.
- We sub-divide it, so now our map has 5 rectangles - one for each quadrant, one for the map as a whole.
- We use a counter to ensure that we don't loop forever (we'll reject a lot of rooms). While we can still add rooms, we:
- Obtain a random rectangle from the rectangles list. Initially, this will be one of the quadrants - or the whole map. This list will keep growing as we add subdivisions.
- We generate a random sub-rectangle inside this rectangle.
- We look to see if that's a possible room. If it is, we:
- Apply the room to the map (build it).
- Add it to the rooms list.
- Sub-divide the new rectangle into quadrants and add those to our rectangles list.
- Store a snapshot for the visualizer.
This tends to give a nice spread of rooms, and they are guaranteed not to overlap. Very Nethack like!
If you cargo run now, you will be in a room with no exits. You'll get to watch rooms appear around the map in the visualizer. That's a great start.
Adding in corridors
Now, we sort the rooms by left coordinate. You don't have to do this, but it helps make connected rooms line up.
#![allow(unused)] fn main() { self.rooms.sort_by(|a,b| a.x1.cmp(&b.x1) ); }
sort_by takes a closure - that is, an inline function (known as a "lambda" in other languages) as a parameter. You could specify a whole other function if you wanted to, or implement traits on Rect to make it sortable - but this is easy enough. It sorts by comparing the x1 value of each rectangle.
Now we'll add some corridors:
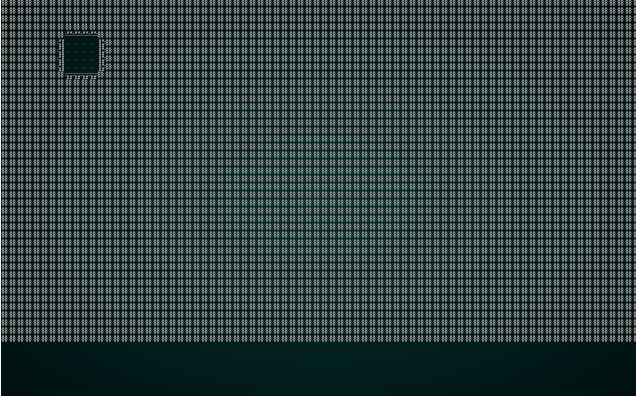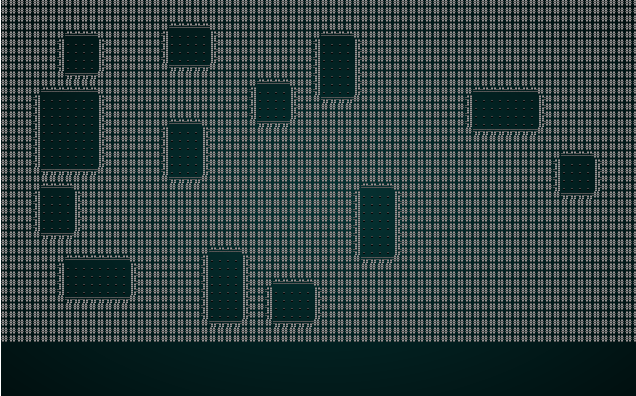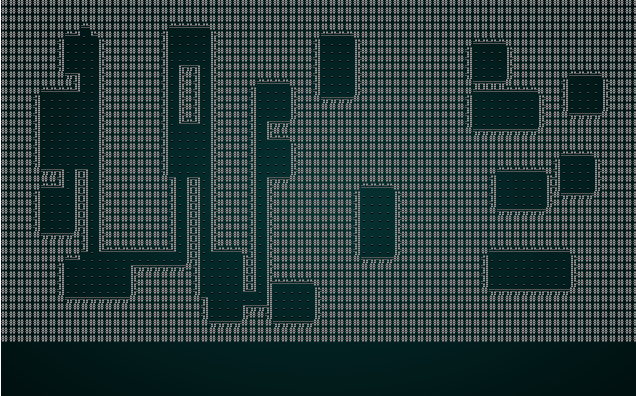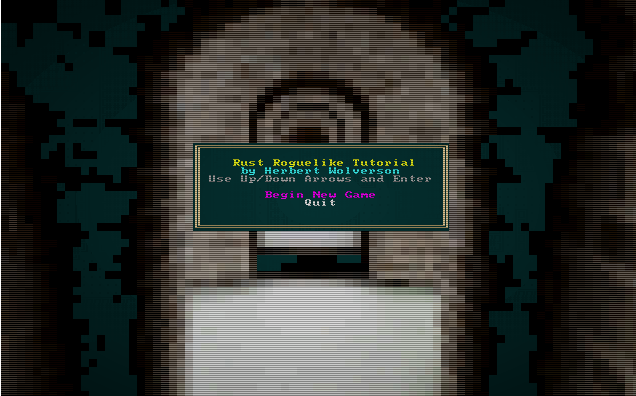
#![allow(unused)] fn main() { // Now we want corridors for i in 0..self.rooms.len()-1 { let room = self.rooms[i]; let next_room = self.rooms[i+1]; let start_x = room.x1 + (rng.roll_dice(1, i32::abs(room.x1 - room.x2))-1); let start_y = room.y1 + (rng.roll_dice(1, i32::abs(room.y1 - room.y2))-1); let end_x = next_room.x1 + (rng.roll_dice(1, i32::abs(next_room.x1 - next_room.x2))-1); let end_y = next_room.y1 + (rng.roll_dice(1, i32::abs(next_room.y1 - next_room.y2))-1); self.draw_corridor(start_x, start_y, end_x, end_y); self.take_snapshot(); } }
This iterates the rooms list, ignoring the last one. It fetches the current room, and the next one in the list and calculates a random location (start_x/start_y and end_x/end_y) within each room. It then calls the mysterious draw_corridor function with these coordinates. Draw corridor adds a line from the start to the end, using only north/south or east/west (it can give 90-degree bends). It won't give you a staggered, hard to navigate perfect line like Bresenham would. We also take a snapshot.
The draw_corridor function is quite simple:
#![allow(unused)] fn main() { fn draw_corridor(&mut self, x1:i32, y1:i32, x2:i32, y2:i32) { let mut x = x1; let mut y = y1; while x != x2 || y != y2 { if x < x2 { x += 1; } else if x > x2 { x -= 1; } else if y < y2 { y += 1; } else if y > y2 { y -= 1; } let idx = self.map.xy_idx(x, y); self.map.tiles[idx] = TileType::Floor; } } }
It takes a start and end point, and creates mutable x and y variables equal to the starting location. Then it keeps going until x and y match end end of the line. For each iteration, if x is less than the ending x - it goes left. If x is greater than the ending x - it goes right. Same for y, but with up and down. This gives straight corridors with a single corner.
Don't forget the stairs (I nearly did!)
Finally, we need to wrap up and create the exit:
#![allow(unused)] fn main() { // Don't forget the stairs let stairs = self.rooms[self.rooms.len()-1].center(); let stairs_idx = self.map.xy_idx(stairs.0, stairs.1); self.map.tiles[stairs_idx] = TileType::DownStairs; }
We place the exit in the last room, guaranteeing that the poor player has a ways to walk.
If you cargo run now, you'll see something like this:
 .
.
Randomizing the dungeon per level
Rather than always using the BSP sewer algorithm, we would like to sometimes use one or the other. In map_builders/mod.rs, replace the build function:
#![allow(unused)] fn main() { pub fn random_builder(new_depth: i32) -> Box<dyn MapBuilder> { let mut rng = rltk::RandomNumberGenerator::new(); let builder = rng.roll_dice(1, 2); match builder { 1 => Box::new(BspDungeonBuilder::new(new_depth)), _ => Box::new(SimpleMapBuilder::new(new_depth)) } } }
Now when you play, it's a coin toss what type of map you encounter. The spawn functions for the types are the same - so we're not going to worry about map builder state until the next chapter.
Wrap-Up
You've refactored your map building into a new module, and built a simple BSP (Binary Space Partitioning) based map. The game randomly picks a map type, and you have more variety. The next chapter will further refactor map generation, and introduce another technique.
The source code for this chapter may be found here
Run this chapter's example with web assembly, in your browser (WebGL2 required)
Copyright (C) 2019, Herbert Wolverson.
